Témou tohto článku je výpočet polykarbonátového vrchlíka vlastnými rukami. Musíme sa naučiť vypočítať hlavné parametre konštrukcie spojené s jej pevnosťou a rozmermi. Tak, poďme.

Čo počítame
Musíme sa naučiť počítať:
- Hrúbka polykarbonátu a rozstup prepravky v závislosti od predpokladaného zaťaženia snehom na meter štvorcový.
- Rozmery oblúkového krytu (čo sa z hľadiska geometrie týka výpočtu dĺžky oblúka).
Pre objasnenie: skúmame spôsoby, ako vypočítať oblúk pre známy polomer a uhol sektora, ako aj pre prípad, keď poznáme iba vzdialenosti medzi krajnými bodmi povrchu oblúka.
- Minimálny prierez potrubia so známym ohybovým zaťažením.
V tomto poradí pôjdeme ďalej.
Hrúbka latovania a povlaku
Začnime výpočtom zaťaženia snehom.
Predtým, ako zistíme, ako vypočítať polykarbonátový vrchlík, sformulujeme niekoľko predpokladov, na ktorých je výpočet založený.
- Uvedené údaje sú relevantné pre kvalitný materiál bez známok deštrukcie ultrafialovým žiarením. Polykarbonát bez UV filtra po 2-3 rokoch prevádzky na svetle skrehne.

- Zámerne zanedbávame obmedzenú deformačnú stabilitu prepravky, pretože ju považujeme za absolútne pevnú.
A teraz - tabuľka, ktorá vám pomôže vybrať optimálnu hrúbku polykarbonátu a rozstup prepravky.
| Zaťaženie, kg/m2 | Rozmery bunky prepravky s hrúbkou polykarbonátu, mm | |||
| 6 | 8 | 10 | 16 | |
| 100 | 1050 x 790 | 1200 x 900 | 1320 x 920 | 1250 x 950 |
| 900 x 900 | 950 x 950 | 1000 x 1000 | 1100 x 1100 | |
| 820 x 1030 | 900 x 1100 | 900 x 1150 | 950 x 1200 | |
| 160 | 880 x 660 | 1000 x 750 | 1050 x 750 | 1150 x 900 |
| 760 x 760 | 830 x 830 | 830 x 830 | 970 x 970 | |
| 700 x 860 | 750 x 900 | 750 x 950 | 850 x 1050 | |
| 200 | 800 x 600 | 850 x 650 | 950 x 700 | 1100 x 850 |
| 690 x 690 | 760 x 760 | 780 x 780 | 880 x 880 | |
| 620 x 780 | 650 x 850 | 700 x 850 | 750 x 950 | |
Arch
Výpočet podľa polomeru a sektora
Ako vypočítať oblúk pre vrchlík, ak poznáme polomer ohybu a oblúkový sektor?

Vzorec bude vyzerať takto P=pi*r*n/180, kde:
- P je dĺžka oblúka (v našom prípade dĺžka polykarbonátovej dosky alebo profilovej rúry, ktorá sa stane prvkom rámu).
- pi je číslo "pi" (vo výpočtoch, ktoré nevyžadujú extrémne vysokú presnosť, sa zvyčajne rovná 3,14).
- r je polomer oblúka.
- n je oblúkový uhol v stupňoch.
Poďme si napríklad vlastnými rukami vypočítať dĺžku oblúka vrchlíka s polomerom 2 metre a sektorom 35 stupňov.
P \u003d 3,14 * 2 * 35 / 180 \u003d 1,22 metra.
V procese práce často vzniká opačná situácia: je potrebné nastaviť polomer a sektor oblúka na pevnú dĺžku oblúka. Dôvody sú jasné: cena polykarbonátu je dostatočne vysoká na to, aby minimalizovala množstvo odpadu.
Je zrejmé, že v tomto prípade sa súčin sektora a polomeru bude rovnať P/pi*180.
Pokúsme sa osadiť oblúk pod štandardný plech dlhý 6 metrov. 6/3,14*180=343,9 (so zaokrúhlením). Ďalej - jednoduchý výber hodnôt s kalkulačkou v ruke: napríklad pre oblúkový sektor 180 stupňov môžete mať polomer rovný 343,9 / 180 \u003d 1,91 metra; s polomerom 2 metre sa sektor bude rovnať 343,9 / 2 \u003d 171,95 stupňov.
Výpočet podľa akordov
Ako vyzerá výpočet návrhu polykarbonátového prístrešku s oblúkom, ak máme informáciu len o vzdialenosti medzi okrajmi oblúka a jeho výške?
V tomto prípade sa uplatňuje takzvaný Huygensov vzorec. Aby sme to mohli použiť, mentálne rozdeľme tetivu spájajúcu konce oblúka na polovicu, potom nakreslíme kolmicu na tetivu v strede.
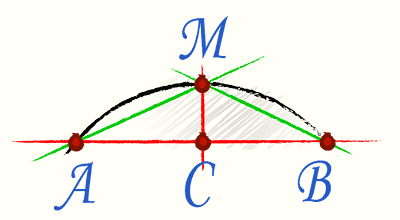
Samotný vzorec má tvar Р=2l+1/3*(2l-L), kde l je akord AM a L je akord AB.
Dôležité: výpočet poskytuje približný výsledok. Maximálna chyba je 0,5 %; čím menší je uhlový sektor oblúka, tým menšia je chyba.
Vypočítajme dĺžku oblúka pre prípad, keď AB \u003d 2 ma AM - 1,2 m.
P=2*1,2+1/3*(2*1,2-2)=2,4+1/3*0,4=2,533 metrov.
Výpočet úseku so známym ohybovým zaťažením
Celkom životná situácia: súčasťou vrchlíka je priezor známej dĺžky. Maximálne snehové zaťaženie na ňom vieme približne odhadnúť. Ako si vybrať profilovú rúrku takejto časti pre nosníky, aby sa pri zaťažení neohýbala?

Poznámka! Zámerne sa nedotýkame toho, ako vypočítať zaťaženie vrchlíka. Hodnotenie zaťaženia snehom a vetrom je úplne sebestačná téma na samostatný článok.
Na výpočet potrebujeme dva vzorce:
- M = FL, kde M je ohybový moment, F je sila pôsobiaca na koniec páky v kilogramoch (v našom prípade hmotnosť snehu na priezore) a L je dĺžka páky (dĺžka nosníka, ktorý nesie zaťaženie od snehu, od okrajových po bodové upevňovacie prvky) v centimetroch.
- M/W=R, kde W je moment odporu a R je pevnosť materiálu.
A ako nám táto kopa neznámych hodnôt pomôže?
Sama o sebe nič. Pre výpočet chýbajú niektoré referenčné údaje.
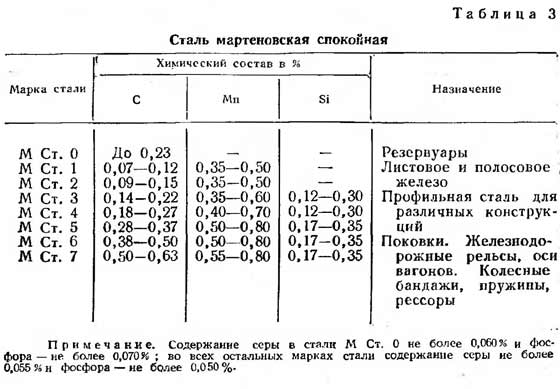
| triedy ocele | Pevnosť (R), kgf/cm2 |
| St3 | 2100 |
| St4 | 2100 |
| St5 | 2300 |
| 14G2 | 2900 |
| 15 GS | 2900 |
| 10G2S | 2900 |
| 10G2SD | 2900 |
| 15HSND | 2900 |
| 10HSND | 3400 |
Odkaz: Ocele St3, St4 a St5 sa zvyčajne používajú na profesionálne rúry.
Teraz, na základe údajov, ktoré máme, môžeme vypočítať moment odporu v ohybe profilovej rúry. Poďme to urobiť.
Predpokladajme, že na dvojmetrovom vrchlíku s tromi nosnými nosníkmi vyrobenými z ocele St3 sa nahromadí 400 kilogramov snehu.Pre zjednodušenie výpočtov sa dohodneme, že celé zaťaženie padá na okraj priezoru. Je zrejmé, že zaťaženie každého nosníka bude 400/3=133,3 kg; s dvojmetrovou pákou sa ohybový moment bude rovnať 133,3 * 200 \u003d 26660 kgf * cm.
Teraz vypočítame moment odporu W. Z rovnice 26660 kgf * cm / W = 2100 kgf / cm2 (pevnosť ocele) vyplýva, že moment odporu by mal byť aspoň 26660 kgf * cm / 2100 kgf / cm2 = 12,7 cm3.
Ako nás hodnota momentu odporu privedie k rozmerom potrubia? Prostredníctvom tabuliek sortimentu obsiahnutých v GOST 8639-82 a GOST 8645-68 regulujúcich rozmery štvorcových a tvarových rúr. Pre každú veľkosť označujú zodpovedajúci moment odporu a pre obdĺžnikovú časť - pozdĺž každej z osí.
Po kontrole tabuliek zistíme, že minimálna veľkosť štvorcovej rúry s požadovanými charakteristikami je 50x50x7,0 mm; obdĺžnikový (s vertikálnou orientáciou väčšej strany) - 70x30x5,0 mm.

Záver
Dúfame, že sme čitateľa nepreťažili množstvom suchých čísel a vzorcov. Ako vždy, ďalšie informácie o metódach výpočtu a navrhovania polykarbonátových prístreškov nájdete vo videu v tomto článku. Veľa štastia!
Pomohol vám článok?